Time & Space Complexity
Analysis of an Algorithm:
- Algorithm analysis is the process of evaluating an algorithm's efficiency.
- The goal is to predict performance without running the program, so it works efficiently for large inputs.
-
The two main aspects of algorithm analysis are:
- Time Complexity - How long an algorithm takes to run as input size increases.
- Space Complexity - How much memory an algorithm uses as input size increases.
Time Complexity
- Time Complexity is the amount of time an algorithm takes to complete as the input size (n) increases.
-
Real World Example:
-
Time complexity can be understood with the example of traveling from your home to the office.
Here, the input size is affected by factors like:
- Traffic lights
- Traffic jams
- Number of stops
-
Now, let's compare different modes of transport:
- Metro - Even if distance increases, the time taken increases slowly. Like a metro, you can reach faster because it has fewer stops and no traffic.
- Bike - Faster than a bus in small traffic but slows down as traffic increases.
- Bus - Takes more time, especially with more stops and heavy traffic, similar to higher time complexity.
-
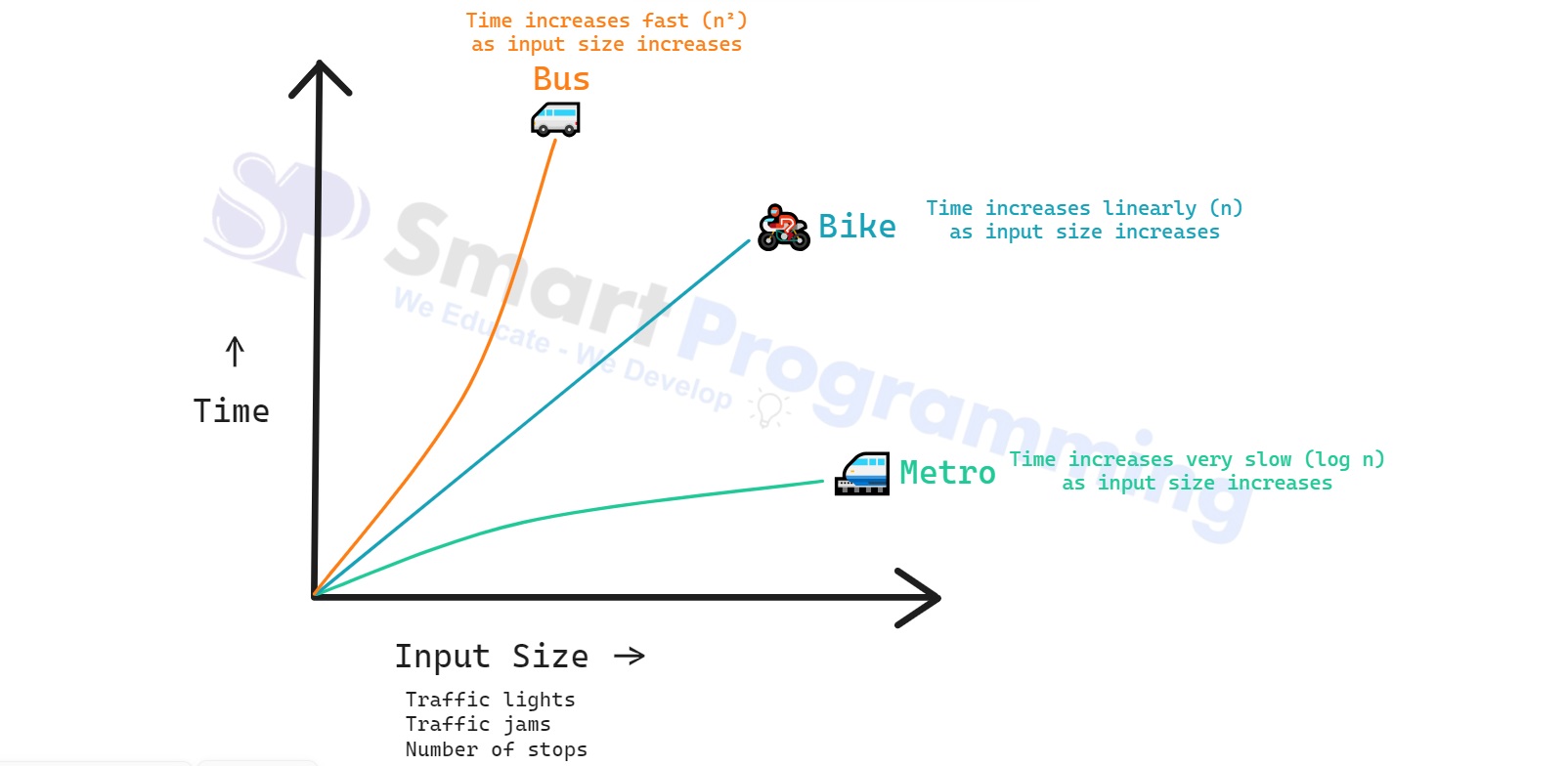
- Conclusion: Just like metro, bike, and bus have different speeds depending on traffic, algorithms have different time complexities depending on input size.
-
Time complexity can be understood with the example of traveling from your home to the office.
Here, the input size is affected by factors like:
-
Project Example :
- There are two shopping applications
- Both use different algorithms to process orders.
-
What is Input Size (n)?
- Input size means the number of items, orders, or data elements the algorithm needs to process.
- Example: In a shopping app, input size could be the number of products ordered during a sale.
- As
nincreases , execution time may increase depending on the algorithm's efficiency.
-
Below is the table showing the time taken by each algorithm for different input sizes (
n):Example Scenario Input Size (n) Algorithm A Algorithm B Small orders (Normal day) 100 orders takes 50 ms of time takes 70 ms of time Moderate sale event 1,000 orders takes 500 ms of time takes 500 ms of time Big festive sale 10,000 orders takes 5,000 ms of time takes 3,000 ms of time Massive flash sale 1,00,000 orders takes 50,000 ms of time takes 15,000 ms of time - As the input size increases, Algorithm A takes more time compared to Algorithm B.
- This means Algorithm B is more efficient for larger inputs.
- Therefore, we can say that Algorithm B has better Time Complexity than Algorithm A.
-
Why Time Complexity is Important ?
- It determines the speed of the algorithm for large inputs.
- It helps to compare the different algorithms for the same problem.
-
How Time Complexity is Measured ?
- Count how the number of basic operations (assignments, comparisons, loops, etc.) grows with the input size n, ignoring constants and machine-specific factors.
-
Use asymptotic notations to represent the growth of time complexity:
- Big O Notation (O) - Describes the upper bound (commonly used for worst-case).
- Omega Notation (Ω) - Describes the lower bound (sometimes used for best-case).
- Theta Notation (Θ) - Describes the tight bound (exact growth, not average case).
-
Common Time Complexities :
-
Below is the table showing common time complexities and their growth rates:
Symbol Name Description Efficiency Notes / Examples O(1) Constant Time Execution time does not depend on input size. ✅ Excellent Accessing an array element, HashMap get()O(log n) Logarithmic Time Time grows slowly as input size increases. ✅ Very Good Binary Search, balanced BST operations O(n) Linear Time Time grows directly in proportion to input size. 👍 Good Traversing an array or list O(n log n) Linearithmic Time Slightly worse than linear but better than quadratic. ⚖️ Acceptable Merge Sort, Quick Sort (average case) O(n²) Quadratic Time Time grows proportionally to the square of input size. ❌ Poor Nested loops (e.g., Bubble Sort) O(n³) Cubic Time Time grows cubically with input size. ❌ Very Poor Triple nested loops O(2ⁿ) Exponential Time Time doubles with every additional input element. 🚫 Extremely Bad Recursive Fibonacci without memoization O(n!) Factorial Time Time grows factorially with input size. 🚫 Worst Generating all permutations -
Below is the chart showing common time complexities and their growth rates:
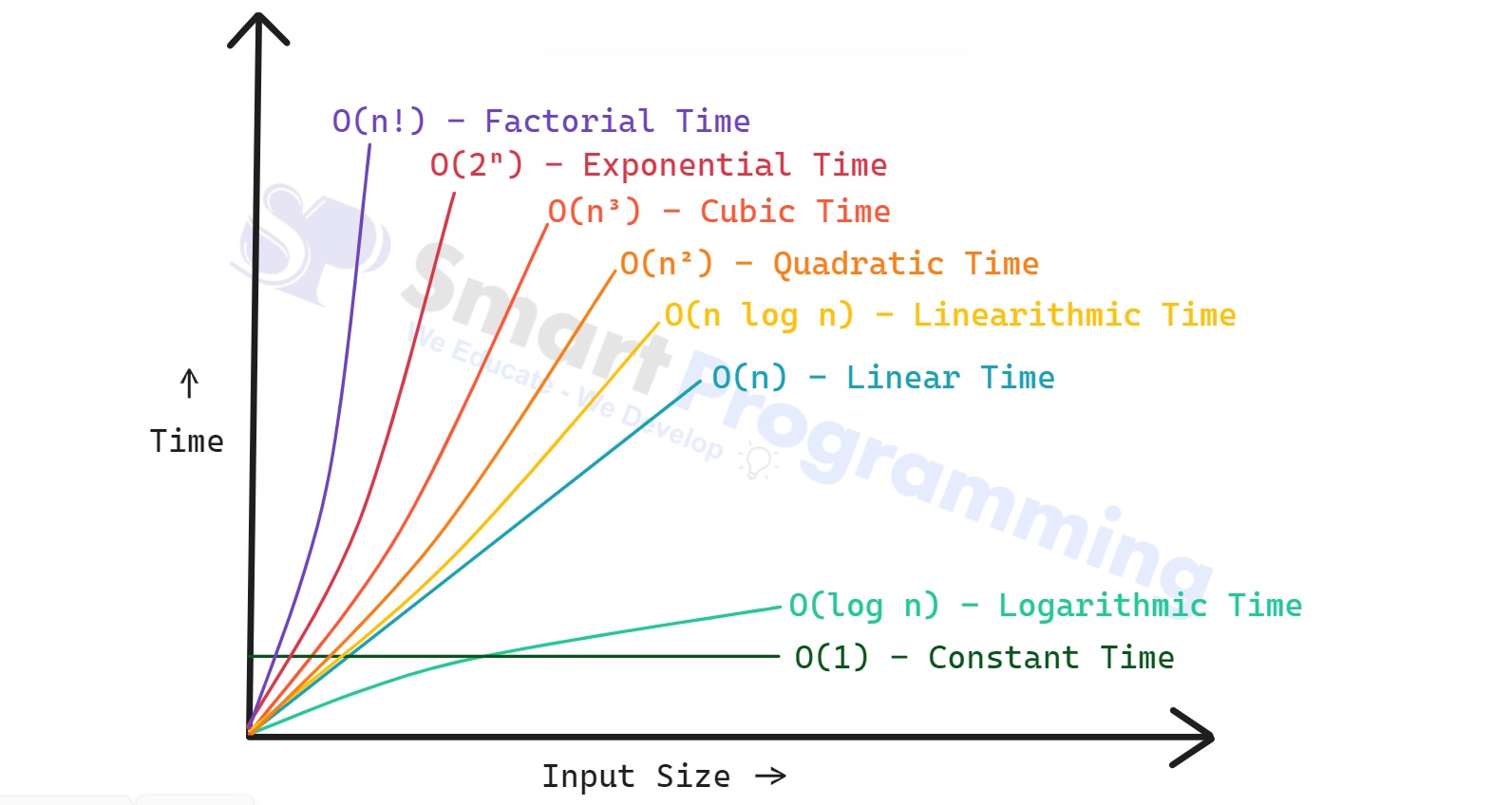
-
Note:
- Here, we have represented all time complexities using Big O notation (O) to denote the worst-case performance of algorithms.
- However, time complexities can also be expressed using Omega (Ω) for the best-case and Theta (Θ) for the average or tight bound scenarios.
-
Below is the table showing common time complexities and their growth rates:
Space Complexity
- Space Complexity is the amount of memory an algorithm uses as the input size (n) increases.
- It includes both the auxiliary space (temporary space used by the algorithm) and the input space (space required to store the input data).
-
Real World Example:
-
Space complexity can be understood with the example of a library.
Here, the input size is affected by factors like:
- Number of books
- Size of each book
- Number of shelves
-
Now, let's compare different storage methods:
- Digital Library - Takes less space as it stores books in digital format.
- Physical Library - Takes more space as it stores physical books.
- Just like digital libraries take less space, algorithms with lower space complexity use less memory.
-
Space complexity can be understood with the example of a library.
Here, the input size is affected by factors like:
-
Project Example :
- There are two photo-editing applications
- Both use different algorithms to apply filters to images.
-
What is Input Size (n)?
- Input size means the size of the image or the amount of data the algorithm needs to process.
- Example: In a photo-editing app, input size could be the file size of the image being edited.
- As
nincreases , memory usage may increase depending on the algorithm's efficiency.
-
Below is the table showing the memory used by each algorithm for different input sizes (
n):Example Scenario Input Size (n) Algorithm X Algorithm Y Small image (Profile pic) 1 MB uses 5 MB memory uses 4 MB memory Medium image (Phone photo) 5 MB uses 25 MB memory uses 15 MB memory Large image (DSLR photo) 20 MB uses 100 MB memory uses 50 MB memory Ultra HD image (Poster) 100 MB uses 500 MB memory uses 300 MB memory - As the input size increases, Algorithm X uses more memory compared to Algorithm Y.
- This means Algorithm Y is more memory-efficient for larger inputs.
- Therefore, we can say that Algorithm Y has better Space Complexity than Algorithm X.
-
Why Space Complexity is Important ?
- It determines the memory usage of the algorithm for different input sizes.
- It helps to choose algorithms that are more memory-efficient, especially for large datasets or devices with limited RAM.
-
How Space Complexity is Measured ?
-
Count how much memory is required by the algorithm, including:
- Memory for input data (input size
n). - Memory for variables and constants.
- Memory for temporary data structures like arrays, lists, or stacks.
- Memory for input data (input size
-
Represent the growth of memory usage with asymptotic notations
- Big O Notation (O) - Represents the worst-case memory usage.
- Theta Notation (Θ) - Represents the average-case memory usage.
- Omega Notation (Ω) - Represents the best-case memory usage.
-
Count how much memory is required by the algorithm, including:
Help Us Get Better Every Day
Your feedback helps us grow! If there's anything we can fix or improve, please let us know.
We’re here to make our tutorials better based on your thoughts and suggestions.